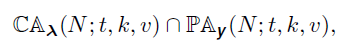Online resource for the computational classifications conducted inBalanced Covering Arrays: A Classification of Covering Arrays and Packing Arrays via Exact Methods
Ludwig Kampel¹, Irene Hiess¹, Ilias S. Kotsireas², and Dimitris E. Simos¹
¹SBA Research, Vienna, Austria
²CARGO Lab, Wilfrid Laurier University, Waterloo, ON, Canada
On this site we collectively present the classification results for (λ,y)-balanced CAs, discussed in the paper entitled "Classification of Covering Arrays and Packing Arrays via a SAT-based Column Extension Approach".
We computed the numbers of non-equivalent CAs appearing in the intersections defining (λ,y)-balanced CAs:
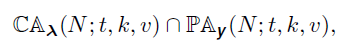
for some t ∈ {2,3,4,5,6}, v ∈ {2,3,4,5,6}, N and all relevant λ, y vectors. For more details please see the paper, e.g. what relevant λ, y vectors means is described in Corollary 1 in the paper.
For these given parameters we compute all non-equivalent CAλy(N;t,k,v) for all t≤ k ≤ CAKλy(N;t,v) as our computational resources permit.
The result of these classifications can be found below in the tables, which are separated for the different alphabet sizes v. The classification results for CAλy(N;t,k,v) for all balance vectors λ and y are retrievable via the hyperlink "Full Classification" in the appropriate row for the given parameters. Additionally, in the column headed by "CAK" we denote the maximal attainable numbers of columns in a CA with the given parameters, independent from balance vectors. In some cases, we can determine the exact value of CAK with the help of inequation (27) of Corollary 1 in the paper, which we indicate by an asterisk, e.g. 12*.
Special attention is being given to (λ,y)-balanced CAs that achieve the maximum number of columns for the given balance vectors, the rightmost column of the "Full Classification" tables so to speak.
For these classification results we create individual tables "CAKλy table" where we fix the number of rows N, strength t and alphabet size v. For some of these tables we have omitted some λ vectors, based on the inequation (27) of Corollary 1 in the paper, which are irrelevant when looking for (λ,y)-balanced CAs that achieve CAK(N;t,v) many columns. We indicate this by an additional asterisk: "CAKλy table*".
The different λ and y vectors appear in the header respectively in the first column of a table.
For specific λ and y vectors, the value of CAKλy(N;t,k,v) appears as bold number in the respective cell of the table and the number of non-equivalent balanced CAs with CAK columns appears as superscript of that.
Whenever the result was obtained by computational search, we denote the required runtime next to it.
When a classification result is obtained by deduction from another result based on a theoretical result, we indicate this with a Greek letter in the "time" column.
The Greek letters refer to the respective bounds of Corollary 1 that are violated.
In these cases the classification result is the same as for the class of (λ,y)-balanced CAs obtained when equality holds in the respective bound(s). Since no computational search is performed for these cases, there is also no time to be reported.
Further, as these deduced results are of limited interest we have reduced the font sizes of the CAKλy# entries, to improve readability of the tables.
The entries labeled "t.o." indicate a timeout, i.e. that the exact classification for the specific instance went beyond our computational resources (in most instances the time limit was set to 3 600 seconds for the computation of one table entry).
When a class of (λ,y)-balanced CAs contains another class for which classification the time limit was reached, we do not attempt its classification as we expect also a timeout for this super-class. In these cases no result is reported and we enter a "-" in the table.
The key to read these tables is given by Table 1, including the mapping between bounds and Greek letters.
Table 1: Key to the 'CAKλy tables': abbreviations and their meaning, for λ=(λ1,...,λt) and y=(y1,...,yt).
| Table entry |
Meaning |
| ω |
reduce y until: yi+1 ≤ yi - (v-1) λi+1, ∀ 1 ≤ i < t |
| κ |
increase λ until: λi+1 ≥ λi - (v-1) yi+1, ∀ 1 ≤ i < t |
| ζ |
increase λ until: λi ≥ N-(vi-1)yi, ∀ 1 ≤ i ≤ t |
| ψ |
reduce y until: yi ≤ N-(vi-1)λi, ∀ 1 ≤ i ≤ t |
| t.o. |
timeout, not finished within 3600 seconds |
| - |
Computation skipped due to previous timeout |
Classification of balanced covering arrays with alphabet size v=2
Classification of balanced covering arrays with alphabet size v=3
Classification of balanced covering arrays with alphabet size v=4
Classification of balanced covering arrays with alphabet size v=5
Classification of balanced covering arrays with alphabet size v=6